Chapter 2
Probabilistic and Statistical Models for Outlier Detection
1 Introduction
概率统计分析方法是最早拿来做异常检测的。最经典的做法就是单变量找极值。但随着多维数据的出现,极值模型不再直接应用在原始数据上,而是对数据做过处理之后,在最后一步输出异常分值,再在上面进行极值检测。可以说通过检测极值把连续型的异常分值转换成二值化的标签(是否异常)。
在不同类型的算法中,以下指标可作为异常分数:
- probabilistic model:数据点与生成模型(generative model)的似然拟合(likelihood fit)
- proximity-based mode:与最近的 k 个邻居的距离、与centroid的距离、局部密度值
- linear model:数据点与数据低维表示的残差距离(residual distance)
- temporal model:数据点与预测值的偏差
2 Statistical Methods for Extreme-Value Analysis
本部分将阐述如何利用概率和统计模型对单变量分布做极值分析。极值在概率分布中被称为分布尾部(tail),而统计模型量化了分布尾部的概率。因此,tail中概率极低的值应视为异常。
2.1 Probabilistic Tail Inequalities
较少假设的不等式能力较弱,但适用范围较广;反之亦反。For example, the Markov and Chebychev inequalities are weak inequalities but they apply to very large classes of random variables. On the other hand, the Chernoff bound and Hoeffding inequality are both stronger inequalities but they apply to restricted classes of random variables.
Markov Inequality
马尔可夫不等式仅适用于非负随机变量,且仅规定了上界
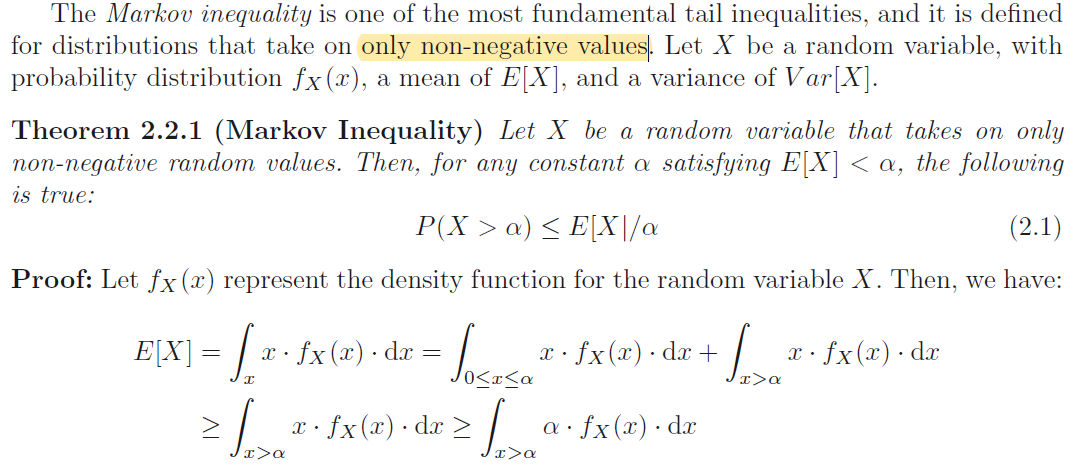
Chebychev inequality
切比雪夫不等式适用于任意变量
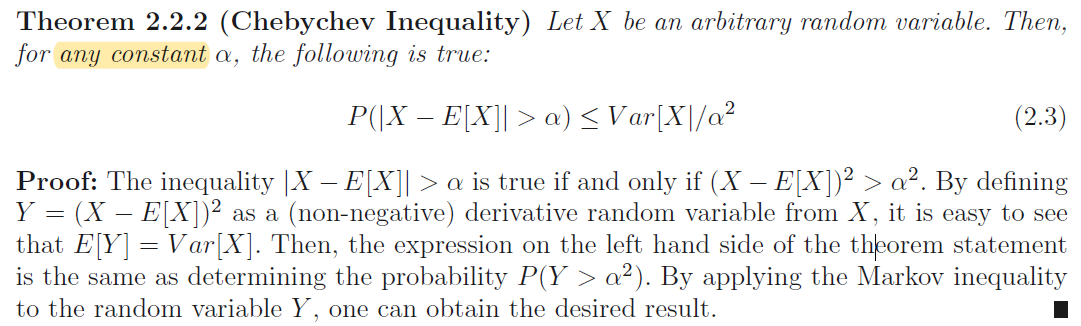
两种不等式只是对数据进行粗略的界定(not provide tight enough bound),这是因为它们对数据的假设较少,马尔科夫只说不是负数就可以,而切比雪夫更没有任何假设,导致这两种不等式在实际应用中很难发挥作用。
而许多变量是以aggregate的形式定义的,可以表述为有界随机变量之和(sums of bounded random variables)
Lower-Tail Chernoff Bound
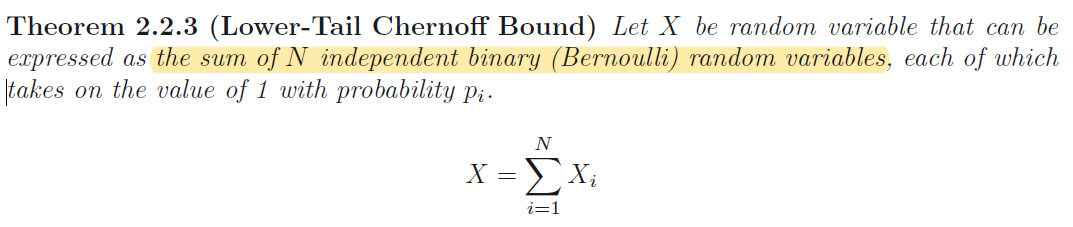
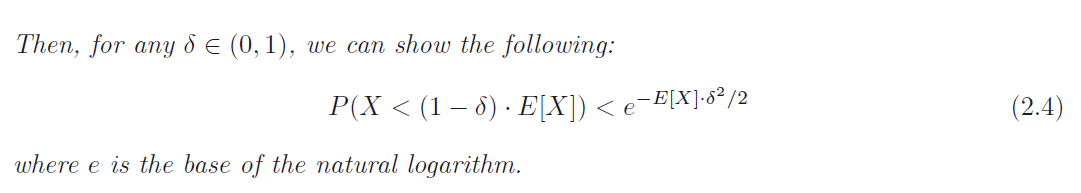

Chernoff Bound假设独立变量服从伯努利,但是接下来要介绍的Hoeffding不等式却没有这个假设,更通用一些。
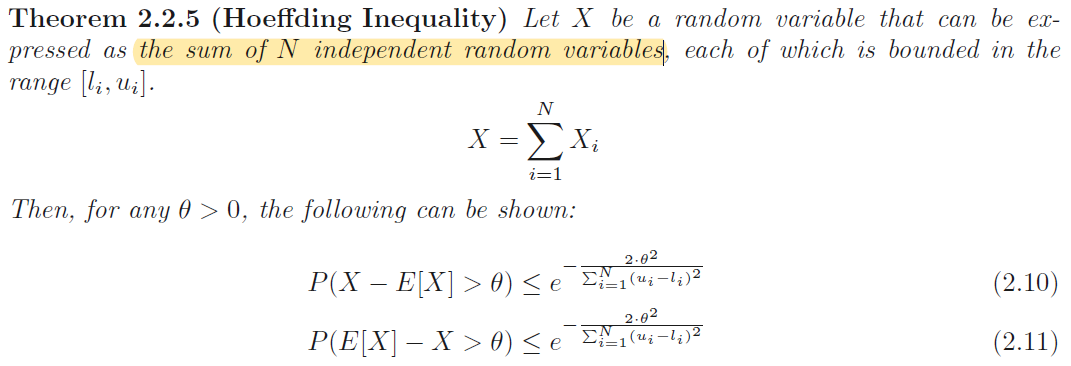
可以看出Hoeffding不等式是Chernoff Bound的更一般形式。下面的表格总结了几种不等式的应用场景及它们的效果。
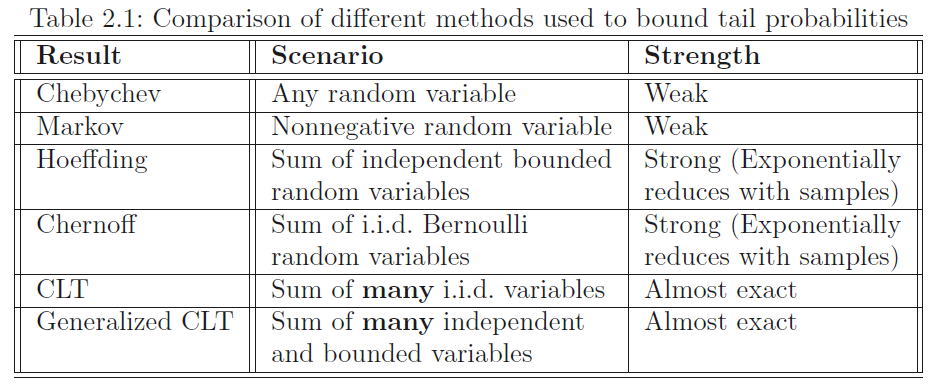
中心极限定理
2.2 Statistical-Tail Confidence Tests
看不懂了不想看了…
