An outlier is an observation which deviates so much from the other observations as to arouse suspicions that it was generated by a different mechanism.

Figure 1.1 (a) 中的数据点A为anomaly，而 (b) 中的数据点A可能是noise分布中的某个点；因此，Outliers 包括 anomaly 或 noise

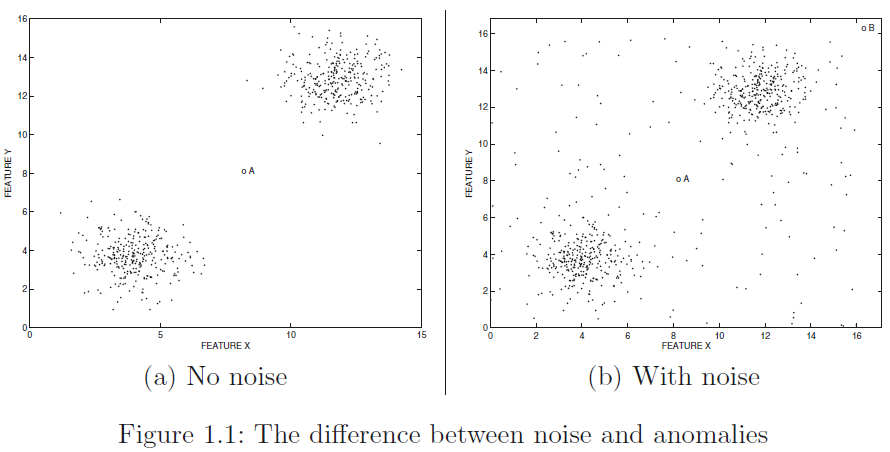
影响异常检测模型建立的因素：数据的类型（连续型，离散型或者混合型等等），数据的多少，异常数据是否能获得（监督学习，无监督学习）以及模型的可解释性。

模型的可解释性是异常检测里极其重要的一部分，当我们尽可能多的使用原始特征，尽可能少的对数据进行变换（PCA降维后特征不具有物理意义），模型的可解释性相对就高一些，反之亦反。

1 Basic Outlier Detection Models

1.1 Feature Selection in Outlier Detection

特征选择可以简述为在无监督学习里如何判断该特征与标签有关

Kurtosis measure (峰值检验)

对于单变量集合 $x_1 \dots x_N$ :

Step1: 计算该集合的均值 $\mu$ 和标准差 $\sigma$ ，并将该集合标准化为位置为0，方差为1：

$z_{i}=\frac{x_{i}-\mu}{\sigma} \tag{1}$

注意 $z_i$ 的平方的均值为1。

Step2：
$K\left(z_{1} \ldots z_{N}\right)=\frac{\sum_{i=1}^{N} z_{i}^{4}}{N} \tag{2}$

非常不均匀的特征分布会显示出很高的峰度。例如，当数据包含一些极值时，峰度度量将由于使用四次幂而增加。

然而，当我们利用峰度分析单一特征时，不能把握特征之间的相互作用，这是该方法存在的一种缺陷。

connections of the outlier detection problem to supervised learning

基本思想是：如果某个特征与其他特征不相关，那么这个特征就被认为和之后的分析无关，因为异常往往是与正常数据训练出来的模型所背离的，所以模型不依赖于这些不相关的特征。

因此，如果利用回归模型，利用其它特征来预测某个特征，当预测误差很大时，那么这个特征就应该被丢弃。在预测时，所有的特征都应该被标准化（sklearn里的StandarScaler），然后选择一个特征当作预测值，利用其它特征来进行预测，评价指标选择RMSE，注意到如果第k个特征的RMSE大于1，那么预测误差就大于特征的方差，该特征就应该被舍弃。也可以用这种方法来对特征加权，第k个特征的权重由max{0, 1-RMSE}决定。

实验：数据利用鸢尾花数据集。在原始数据的基础上，随机产生一列特征，加入到原始数据里，然后把每个特征当作预测值：

from sklearn.datasets import load_iris
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import mean_squared_error
import numpy as np
from sklearn.preprocessing import StandardScaler

iris_data = load_iris().data
target = load_iris().target
# print(iris_data.shape) #(150, 4)
feat_random = np.random.random(iris_data.shape[0])
# 新数据集的特征shape为(150,5)
mergerd_iris_data = np.concatenate((iris_data, feat_random.reshape(-1, 1)), axis=1)
scaler = StandardScaler()
data = scaler.fit_transform(mergerd_iris_data)

for i in range(data.shape[1]):
    lr = LinearRegression()
    y = data[:, i]
    x = np.delete(data, i, axis=1)
    # cross_val_score：得到K折验证中每一折的得分，K个得分取平均值就是模型的平均性能；计算的是k个得分
    # cross_val_predict：得到经过K折交叉验证计算，得到的每个训练验证的输出预测（从fold 1-k 顺序保存）；计算的是y个预测值
    y_predict = cross_val_predict(lr, x, y, cv=5)
    error = mean_squared_error(y, y_predict, squared=False)
    print("其他特征预测第%d个特征时，RMSE的值是：%.3f" % (i, error))
    """output
    其他特征预测第0个特征时，RMSE的值是：0.394
    其他特征预测第1个特征时，RMSE的值是：0.743
    其他特征预测第2个特征时，RMSE的值是：0.196
    其他特征预测第3个特征时，RMSE的值是：0.266
    其他特征预测第4个特征时，RMSE的值是：1.025
    """

1.2 Extrem-Value Analysis

极值检测是异常检测最基础的一种形式，其目的在于将那些太大或者太小的值视为极值。但有时，异常值和极值并不相同，举个栗子，在数据集{1, 2, 2, 50, 98, 98, 99}中，最小值1和最大值99被认为是极值，而基于概率或密度的异常检测模型则认为50为异常值，因为其不属于两个子集合{1, 2, 2}和{98, 98, 99}。

然而，极值通常在异常检测算法的最后一步中起着重要的作用，这是因为大多数的异常检测算法使用异常得分来衡量数据的异常水平。

1.3 Probabilistic and Statistical Models

在概率和统计模型中，关键是假设数据的分布，利用数据的分布进行建模然后再学习模型的参数。对于特定的分布就有较低 fit value 的数据点被归为异常

这种模型的优点是它能适应各种类型的数据。离散型变量就用伯努利分布，如果是混合变量，就可以用针对每个不同特征的分布来做一个乘积。
缺点也是显而易见的，就是它的假设是数据符合某种分布，这个是不太合适的；此外，随着参数的增多，会产生过拟合现象；可解释性较差

1.4 Linear Models

线性模型是在低维空间里利用线性相关性对数据进行建模。通常是对正常数据进行回归分析，利用最小二乘法确定最佳的超平面。

对于一个二维的数据来说，我们一般用下面这个公式来对它进行拟合。

$y_{i}=a \cdot x_{i}+b+\epsilon_{i} \quad \forall i \in\{1 \ldots N\} \tag{3}$

其中 $\epsilon_{i}$ 为残差，表示建模误差，参数 a 和 b 从数据中学习而来，以最小化least-squares error $\sum_{i=1}^{N} \epsilon_{i}^{2}$ 。利用残差平方和来评估数据的异常程度，这时候极值分析也可以用在残差上，残差大的可以当作是异常。

PCA 是一种无参数的方法，通过最小化重构误差，来将数据投影到低维度的子空间。因此重构误差可用于检测异常数据；此外，PCA还可以用于噪声恢复（noise correction），在这个过程中，异常值更有可能被大幅度的恢复。

降维和回归模型的可解释性也较差。但是有一些降维方法，如说非负矩阵分解，具有很好的解释性。

1.5 Proximity-Based Models

基于邻近度的模型通过相似性或者距离函数把那些远离其他点的数据当作异常点，它是异常检测最流行的一种模型，主要有基于聚类、基于密度和最近邻的方法。

聚类和基于密度的异常检测主要区别是聚类是对数据点进行分割，基于密度的方法比如直方图法是对数据空间进行分割。这是因为后者的目的是检查数据空间里待测试点的密度，所以利用空间分割的方法是较好的。但是，如果异常点聚堆的话，那么对基于密度的方法来说，可能会识别不出来。

在最近邻模型当中，每个数据点到它最近的k个邻居之间的距离可以被认为是异常得分。要得到每个数据点的异常得分，计算量会很大。它要计算每个数据点与它k个最近邻的距离，时间复杂度是n²，如果我们只需要知道这个数据点是不是异常（是或者不是），计算速度就高效多了，即确定在计算到一定程度时，确定该数据点一定不是异常，便可终止计算。
在基于聚类的方法里，第一步首先是利用聚类算法来确定数据集中的密集区域，第二步是在每一个cluster里应用一定的方法来确定异常分值。比如说在 K-means 聚类里，每一个点到它所在cluster的质心之间的距离，可以当作异常分值。需要注意的地方是聚类的方法不同，对最后结果也有影响，通常是运行许多次聚类算法，然后对结果求平均，这样得到的结果往往robust。
基于密度的方法如直方图，将数据空间划分为小的区域，然后区域中数据点的数量被用于计算异常分数。基于密度的方法具有很高的可解释性。例如异常区间：Age ≤ 20, Salary ≥ 100, 000，便很好的解释了为什么异常

1.6 Information-Theoretic Models

基于信息论模型进行异常检测的思想是，异常值会增加对信息进行编码的长度，如下两个字符串：

ABABABABABABABABABABABABABABABABAB
ABABACABABABABABABABABABABABABABAB

第二行将第一行中的C替换为了A，对于第一行，可以用“AB 17”来编码，而第二行的编码要复杂，即增加了正常信息的最小编码长度。实际上，基于信息论的方法与传统方法是相似的，都是使用数据的简洁描述作为基准来进行比较：

在信息论模型里，最关键的是构建密码本（code book）来表示数据。如果移除某个数据后，code length减少最多，那么这个数据极有可能是异常值。

1.7 High-Dimensional Outlier Detection

在高维空间里，有些特征是噪声或者跟我们想要的异常并不相关，而且，在高维空间里，点与点之间的距离都是很相近的。在这种情况下，异常值往往在局部子空间下表现的很明显，局部子空间的特征也有相关性，但是在full-dimensional下，这种异常模式会被掩盖。有时候我们会对很多个子空间进行异常检测，将结果再合并起来，找出更有代表性的异常值，这种方法又叫outlier ensemble。

2 Outlier Ensembles

分类问题中的ensemble方法包括：bagging，sub-sampling，boosting 和 stacking，集成方法同样可以用到聚类和异常检测中，异常检测中的ensemble方法主要分为两类：

Sequential Ensemble：将算法顺序堆叠，最终的结果可以是不同算法的加权组合，也可以是最后一个算法的输出。下图为线性集成方法的算法框架，每次迭代，基于之前的运行结果，后续改善过的算法会应用在改善的数据集上。

Independent Ensemble：不同的算法，或者相同算法的不同实例，应用于数据集或子数据集；算法执行过程相互独立，最终进行聚合以获得更加robust的离群值。下图为独立集成方法的算法框架，此类方法的基于的思想是：不同的算法在数据的不同部分上可能会表现更好。该方法经常用于高维数据的离群值检测，因为这样可以充分探索数据的不同子空间。

3 The Basic Data Types for Analysis

真是数据往往是混合特征的，既包含类别特征，又包含数值特征。而文本特征中又会包含时序关系。

Times-Series Data and Data Streams

对于时间序列的异常，文中举了以下例子：

3, 2, 3, 2, 3, 87, 86, 85 87, 89, 86, 3, 84, 91, 86, 91, 88

在时间戳6上，数据从3突变到87，这个变化就属于时序上的异常，紧接着，数据在87上下浮动，又变成了一种新的正常模式，在时刻12上，数据又突变到3，虽然数据3之前出现过，但是仍然被当作异常，因为它属于连续数据突变的情况。因此，数据是上下关联的，如果把数据分割开来对异常检测没有任何意义。换句话说，时间语境很重要。关于时序数据的变化，可以分为以下两种情况：

数据值和趋势随时间缓慢变化（concept drift，UNICORN在检测APT攻击时提到过这个概念，以此表示APT攻击缓慢的攻击行为）
数据值的突变

对于时序数据异常检测最大的挑战是：实时检测

Discrete Sequences

许多入侵检测、欺诈检测和生物序列都是离散序列，即时序数据中每个位置是离散的类别值，而不是连续的数值数据

Spatial Data

Network and Graph Data

图数据的异常对象可以是节点、边或整张图。

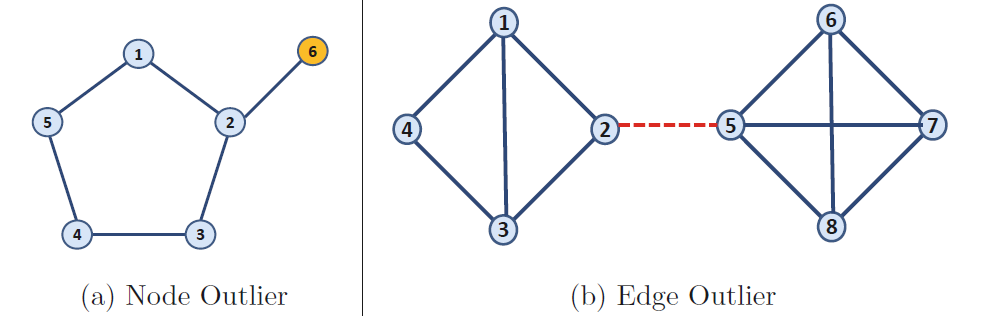
也可以组合不同类型的依赖关系进行建模。例如，图本可以是时序的。在这种情况下，数据可能同时具有结构和时间上的依赖关系，这些依赖关系会随着时间的变化而相互影响。

4 Supervised Outlier Detection

当标签可用时，尽量使用有监督学习，因为监督学习的效果要好于非监督学习。

有监督的异常检测与分类问题最大的区别在于，异常检测的数据往往是极度不平衡的，所以一些检测器即使把所有数据都分类为正常，其检测准确度也非常高，但这往往是没有实际意义的。所以我们需要调节检测器，使其在异常数据上分类错误的惩罚程度要高于在正常数据上的分类错误的惩罚程度，即宁要false positive，不要false negative。

监督学习下的异常检测存在以下挑战：

Positive-Unlabeled Classification (PUC) ：可使用的异常数据量有限，而正常数据中可能包含未知比例的异常数据
仅仅有异常数据和正常数据的某个子集可用于模型训练，而一些异常类别在训练时可能没有见过；这种情况在入侵检测中尤为常见因此需要结合有监督和无监督方法，采用半监督方式
在主动学习中，对离群值标签的查询十分昂贵

5 Outlier Evaluation Techniques

false positive 和 false negative 之间的权衡可以用 precision 和 recall 来度量：

高precision有时候会导致低recall，反之亦然。在知道如何计算precision和recall之后，通过调节阈值t，可以得到一系列precision和recall，并画出precision-recall（PR）曲线。

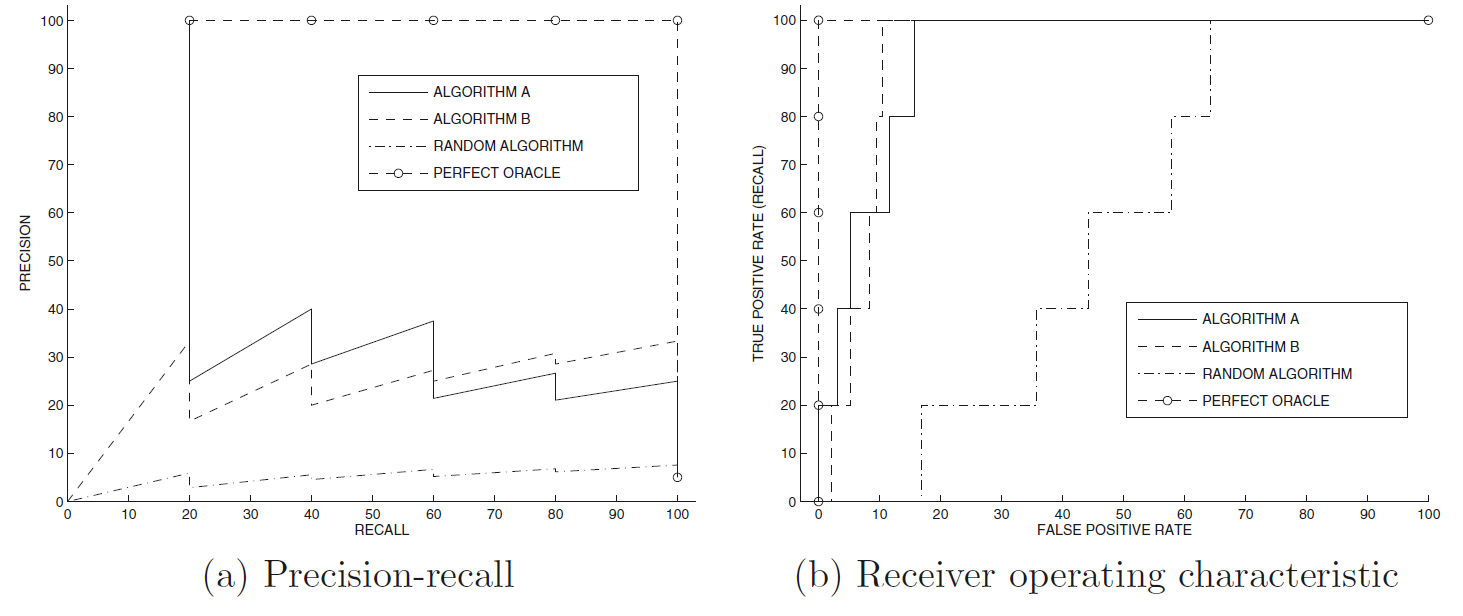
ROC曲线：

更多时候我们计算ROC曲线下的面积，即AUC，通过比较AUC来判别算法模型的好坏。可以这样理解AUC：随机选取一个异常样本和一个正常样本，异常样本排在正常样本之前的概率即AUC。

在对比两个异常检测算法的时候，有一种常见的错误，就是我们会利用数据进行模型调参，让AUC达到最优。由于引入了人为先验，算法就不能算是无监督的了。通常的做法是让参数在一个合理的区间内，运行算法，根据变化的参数，使用一些central estimator来评估性能。而对不同的算法来说，其最佳的参数范围又是不确定的，这为对比两个算法造成了进一步的阻碍。

一个想法是，能否用每个模型的最佳参数来进行对比，但这样做会存在两个问题：（1）无监督情况下是无法得知最佳参数的；（2）只比较最佳参数，会偏爱那些不稳定的模型（稳定模型平均情况好于不稳定模型，而不稳定模型在特定参属下过拟合导致效果极好，优于稳定模型）。对于这种情况，可以对不同参数设置下的模型表现取平均后，比较他们的 ensemble AUC。