原文标题：Analysis of high volumes of network traffic for Advanced Persistent Threat detection

原文作者：Mirco Marchetti, Fabio Pierazzi∗, Michele Colajanni, Alessandro Guido Department of Engineering “Enzo Ferrari”, University of Modena and Reggio Emilia, Italy

原文来源：Computer Networks 2016

原文链接：https://fabio.pierazzi.com/papers/pierazzi_apt.pdf

1 摘要

本文提出的方法可以通过分析大量的网络流量，揭示与APT的数据窃取或其它可疑行为相关的弱信号。最终的结果是呈现一个对网络内部主机的排名，从而安全分析人员可以将注意力放在少数几个可以主机上。

2 简介

2.1 研究现状

• 传统的安全方案是基于模式匹配的，但这种方法只能检测已知攻击，但对于经常利用未知漏洞、标准协议和加密通信的APT来说难以奏效。
• 现存的流量分析技术只能够检测普通的攻击（如DDos），但是由于APT攻击者会模拟正常行为、仅入侵有限数量的主机，所以能够避免被检测到。
• 在大型的网络系统中，其产生的报警数量是非常庞大的，而且基于主机的日志（如系统调用）的收集和分析也会非常昂贵，因此本文着眼于网络流量进行分析

2.2 研究目标

注意，本文的研究目标不在于非常明确的值除哪台主机被攻击了。而是在一个具有上千台主机的环境中，能够挖掘出少数几台具有可疑行为的主机。

2.3 方法和贡献

本文提出的框架能过够收集并分析大量的流量，检测与数据窃取相对应的APT活动的关键阶段。通过检查每个主机的过去，并将其与其他主机进行比较，来评估每个主机的可以移动和位置。 最终输出是主机的排名列表，安全分析人员可以将其注意力集中在top-k可疑主机上。

效率提升：通过分析网络流（network flow）而不是原始的流量数据

可扩展性：由于不需要监视数据载荷（payload），该方法甚至能工作在加密的通信中

主要贡献如下：

• 描述了真实大型网络环境中的网络统计数据，并定义了一个模型，旨在检测APT相关活动，并特别关注数据窃取；
• 定义了一系列算法，通过评估多维特征空间中主机随时间的移动和位置，对疑似APT的活动进行打分
• 设计并实施了一个prototype，将其应用于一个包含10K台主机的环境中

3 相关工作

我们的方法是，将基于与已知APT知识的启发式方法，和能够捕获可疑网络活动的行为统计模型相结合。

基于现在的研究情况，我们可以从下面三个方面来考虑。

3.1 APT检测

分析APT案例、提出形式化描述（7-phase、攻击金字塔）、基于图分析、异常检测系统、数据窃取检测

3.2 僵尸网络检测

对僵尸网络的检测是分析大量具有相似行为的主机，而APT受害网络中可能仅包含少数受害主机，所以不能用检测僵尸网络的聚类分析方法来检测APT受害网络。

另外，二者的感染策略也是不同的。

3.3 内部威胁

内部威胁与APT攻击也有相似之处，但不同在于内部威胁在进行数据窃取时，可能不需要通过网络，因此检测内部威胁多集中于主机日志或者蜜罐策略上。而本文提出的框架，可以轻松集成到内部威胁检测系统中。

4 APT生命周期

下面我们分析APT的各个攻击阶段，阐述其为什么能够用网络流量来分析：

• reconnaissance phase：寻找网络的可能入口点，会进行扫描操作
• compromise phase：在目标系统在安装恶意软件RAT：Remote Access Trojan、 Remote Administration Tool
• maintaining access phase：RAT联接C&C服务器来接受攻击者的指令。值得注意的是，这个阶段的网络连接是由受害者主机发起的，而不是攻击者。这样做的目的，一是骗过防火墙；二是攻击者因此会减少被检测到的机会，这是因为从外部网络下载内容会被高度怀疑。
• lateral movement phase：攻击者想要获得其它主机的访问权限。如RAT可能会进行内部的扫描，或者试图与组织内部的其它主机建立新的连接。
• data exfiltration phase：被窃取的数据被发送到攻击者控制的远程服务器。这个过程有可能是一次性迅速（burst）完成的，也有可能是慢速（low-and-slow）的。

5 APT检测的挑战

• 不平衡的数据（Imbalanced data）：在巨大量的数据中，APT只占很少一部分，因此使得攻击难以检测
• Base-rate问题：APT相关的事件非常少，而且时间跨度很长，因此会带来恒奥的误报率。
• 缺乏公开数据
• 加密和标准协议（例如HTTPS）的使用会阻碍常用的网络安全解决方案，例如基于签名的入侵检测系统。

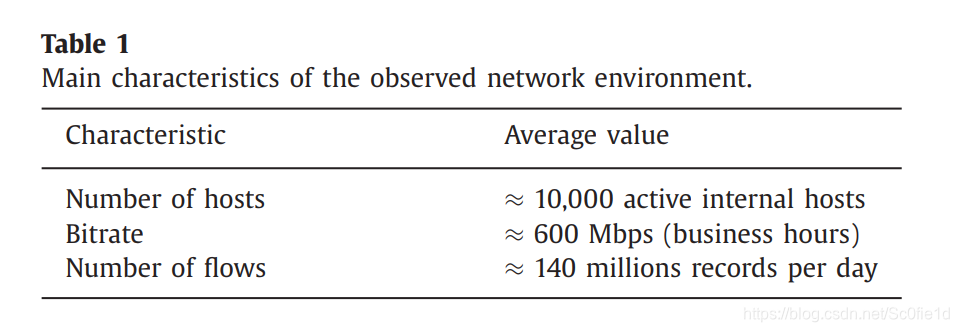
下图是10k个主机环境中的网络统计情况：

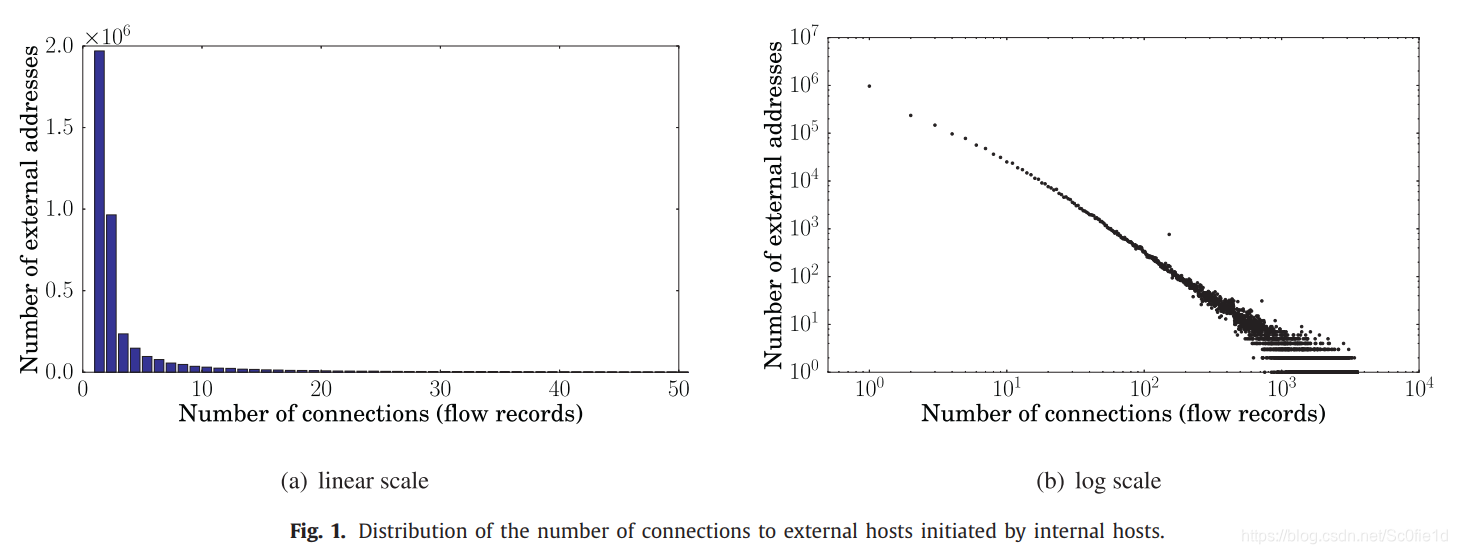
(a)和(b)分别是对同一分布的不同描述，从图(a)中可以看出该分布属于重尾分布。该图表示从内部主机向外部IP地址建立连接的数量，事件跨度是一天。如在图(a)中，第一个直方图表示有大约2M个IP地址仅仅被连接了一次，第二个直方图表示有大约220K个IP地址仅仅被连接了3次。因此我们可以得出结论：大多数外部主机仅被连接一次或几次。

出现这种现象的原因与云计算的广泛应用有关。即使是在很短的时间内，与外部地址连接的总数也相当高，但是大部分的外部地址仅仅被连接了很少几次。这样的结果是不希望看到的，这样的连接情况会连接多个不同的云计算提供商。

针对该问题前人的一些方法：

• 为所有的云计算提供商设置白名单；但这样攻击者很容易创建一个云账号来作为C&C服务器或者数据窃取点
• 基于阈值：效果不佳，因为无法为这种重尾分布设置合适的阈值
• 聚类：这会将数据聚成两类，一类是头一类是尾
• 箱线图规则（boxplot）：这对于离群值检测无效，因为基础分布不是高斯分布

于是，本文提出的方法将单个主机的行为建模，将其作为多重特征空间中的特征点；然后比较主机的统计信息，包括它们的过去以及所有其他内部主机的统计信息；然后为每个内部主机分配一个分数。

6 框架概览

本文所提方法的特点如下：

• 基于流量信息，这些数据通过网络探针可以很容易地获得
• 提取并分析流量记录，这使得存储和计算消耗都有所降低
• 通过下面两方面来识别执行可疑活动的主机：
  • 分析他们之前的行为
  • 分析其他主机的行为
• 提出了一些特征，用于识别可能与数据窃取有关的主句
• 所提出的“排名”的方法，不依赖于深度包检测，因此可以运行在加密的流量上

本文所提出的系统架构如下图所示，其工作过程包括5个阶段：

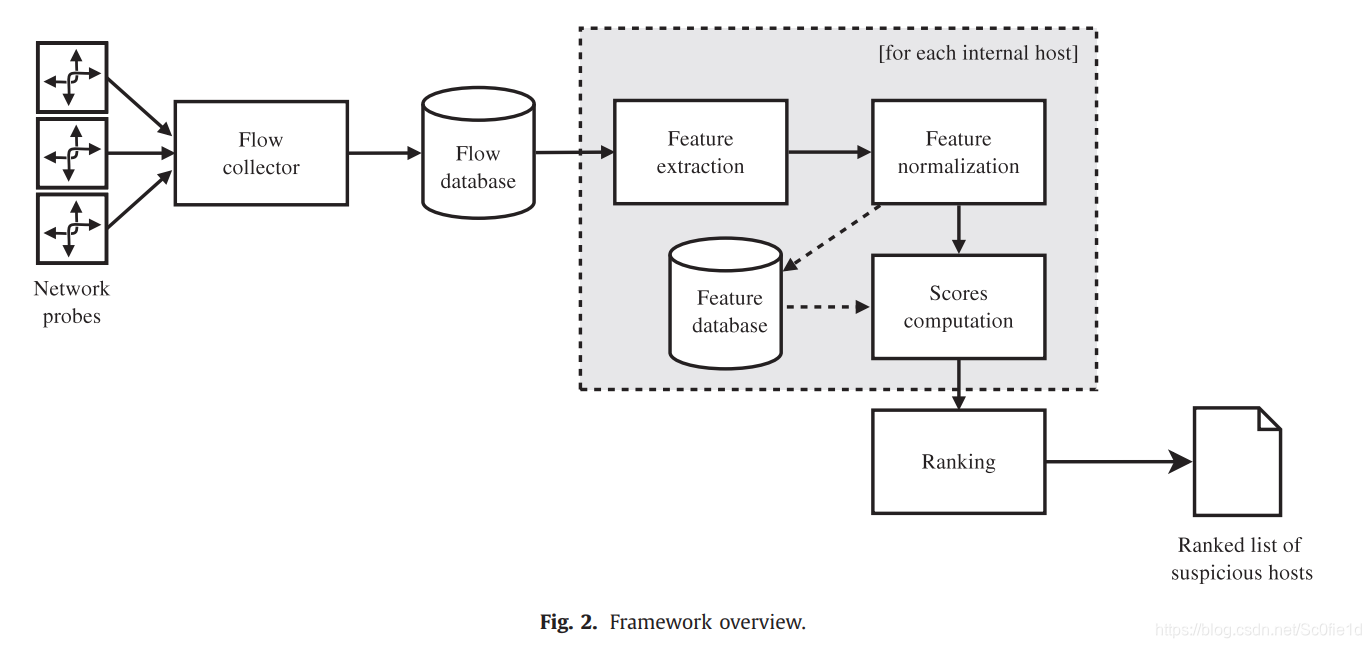
（1）流量收集和存储：不使用原始的流量数据（raw traffic data），而是使用流量记录（flow record）；每条记录包含从IP头部中提取的数据，包括：源、目的地址和端口号，协议类型。这样做对系统性能有很多好处：

• 易于存储和压缩

• 计算上更可行

之前我们说，假设所有与外部的连接都是由内而外发起的，所以我们仅仅考虑出站流量，即从内部发往外部的流量。而从外部发往内部的可以用传统的IDS来检测

（2）特征提取：提取与数据窃取相关的特征，特征在每台主机上每隔时间T计算一次。特征提取工作由专用服务器完成。

（3）特征归一化：将不同的特征归一化，因为每个特征都有不同的重尾分布，因此处于比较目的，必须将其归一化。这一步的实现由参考文献[45]中的归一化度量完成，这种方法专用于归一化具有不同特征的重尾分布。

（4）可疑分数计算：对于每台主机，每个时间$t_{i}$，该阶段涉及与特征空间中主机行为有关的统计信息的计算，为此我们考虑三个点：

• 当前时间$t_{i}$时，主机的特征值
• 历史窗口W下（$t_{i-1-W}$到$t_{i-1}$），同一主机的标签值的质心（centroid）
• 时间$t_{i}$时，所偶有主机的特征值的质心

历史窗口表示主机过去的行为。考虑了最近过去（recent past）的运动方向，因此沿罕见方向的运动被认为是可疑的。

（5）排名：可疑程度通过以下方式的线性组合进行评估：

• 内部主机相对于特征空间质心的归一化距离
• 运动幅度的增长百分比
• 相对于所观察的网络环境中所有内部主机的运动而言，运动方向的不可能度。

我们注意到，第2、3、4个阶段可以在每台主机上独立并行执行。

7 特征提取和归一化

7.1 特征提取

定义：

• $H_{I}$和$H_{E}$分别表示内部和外部主机的集合
• 对于每个内部主机$h \in H_{I}$，特征向量$\mathbf{x}_{t}(h)$由下面的元组定义：

$\mathbf{x}_{t}(h)=\left(x_{t}^{1}(h), x_{t}^{2}(h), \ldots,x_{t}^{N}(h)\right)$，其中$x_{t}^{i}(h)$对应时间$t$时，内部主机$h$特征向量的第$i$个组成部分的值；另外$x_{t}^{i}(h)$每隔一个取样周期$T$计算一次，据此来建立一个时间序列。

我们将时间粒度$T$设置为1天，原因如下：

• APT攻击时间跨度较长，设置太细的时间粒度的话，会产生很多噪声
• 每天产生一次排序列表，有助于分析人员进行分析

下面，我们定义了一系列的特征：

• numbytes：由内部主机上传到外部地址兆字节（megabytes）数。用来监视上传字节的偏移（deviations of uploaded bytes），因为这有可能跟数据窃取有关。例如，如果主机的upload字节数增加了十倍，则它可能参与了APT相关的活动。
• numflows：内部主机发起的连接到外部主机的flow数量。用来监视由内部主机发起的数据传送。由内部主机发起数据泄露有如下两个原因：(i)向外的连接大多数防火墙都不会拦截；(ii)外部主机发起的连接会很容易被传统的IDS蓝饥饿
• numdst：内部主机发起的连接中，外部IP地址的数量。用来检测那些包含许多变化的目的IP的异常行为，这些连接同样是由内部主机发起的。例如。进行通信的外部IP数量稳定，但是upload字节数或者连接数却急剧上升，这就很有可能发生了与数据窃取相关的APT活动。

我们意识到，正常情况下，numflows和numdst几乎是同步增减的。虽然在机器学习中，建议我们尽量选取不相关的特征来获取更多信息，但是我们的问题并不是一个分类问题，因此我们选择两个相关的特征，来捕获那些违反了numflows和numdst之前预期关系的主机。

下图是本文所用数据的特征分布情况：

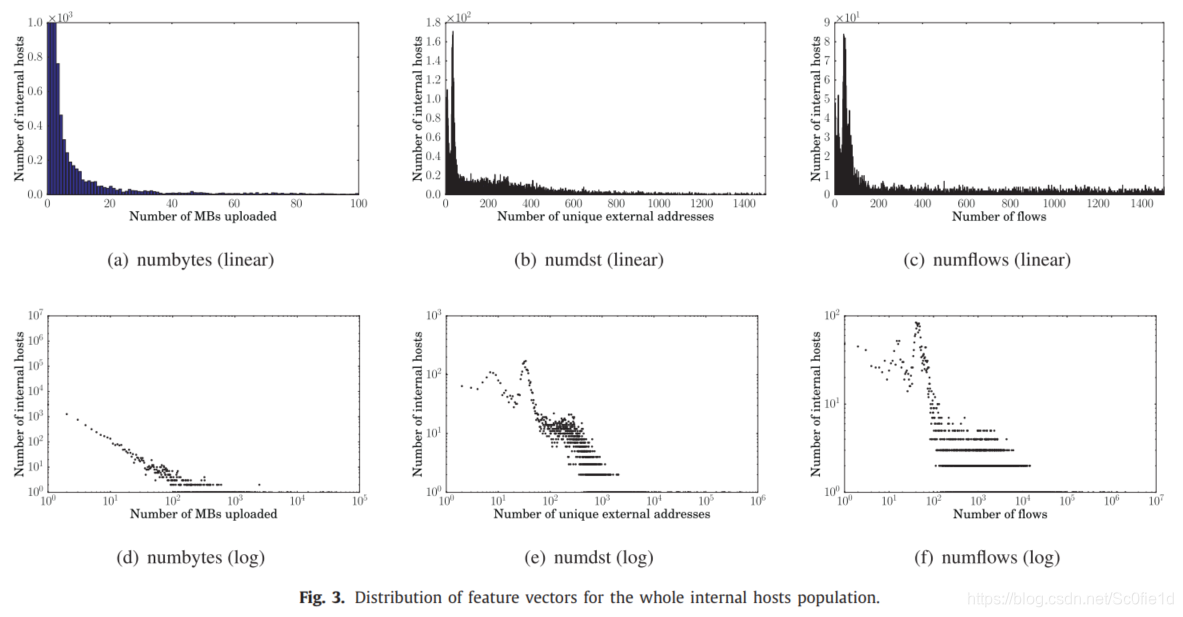
下图是特征空间的3D表示，

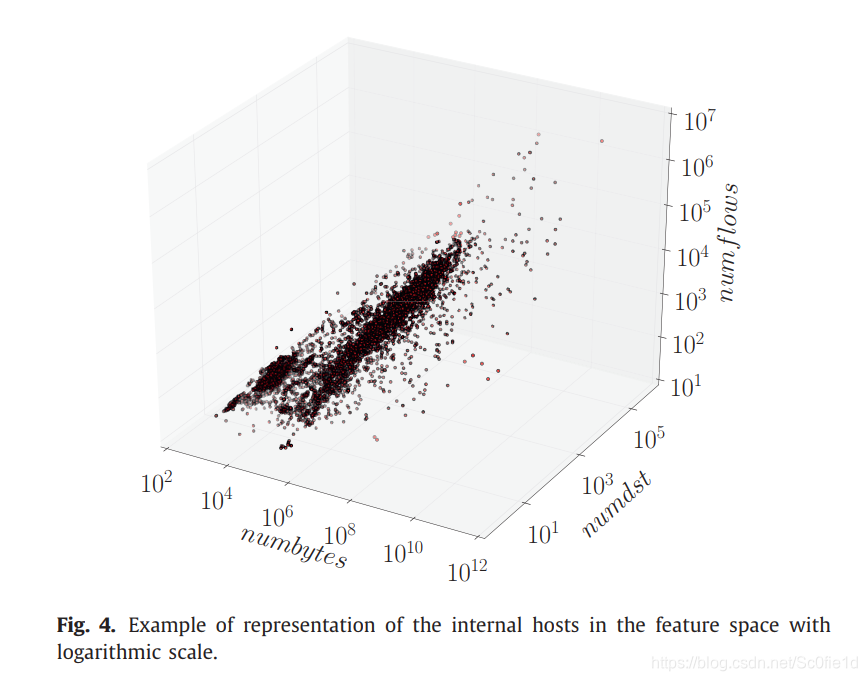
通过监视主机的移动和他们与过去、与特征空间质心之间的举例，来检测异常主机。

7.2 特征归一化（Normalization）

为了公平地比较内部主机的移动和位置，必须对其分布进行归一化。

一种方法是range归一化，即将数据映射为0到1之间的数。但是对于重尾分布来说，这种方法会导致大部分数据都接近于0。

为了解决这个问题，本问提出了双边四分位数加权中位数（two-sided quartile weighted median，QWM）指标：

$Q W M(D)=\frac{Q_{75}(D)+2 \cdot Q_{50}(D)+Q_{25}(D)}{4}$

其中，$Q_{k}(D)$表示数据集$D$中的$k$分位点。该度量既考虑了中位数（$Q_{50}$），又考虑了由第一和第三四分位数表示的数据方差。这使得QWM具有鲁棒性，并独立于数据分布，同时也适用于归一化后的重尾分布。

对于 t 时刻主机 h 的特征向量$\mathbf{x}_{t}$ ，将其归一化之后用$\overline{\mathbf{x}}_{t}$表示。归一化操作为对其每个组成部分$x_{t}^{i}, \quad i \in\{1,2, \ldots, N\}$做如下操作：

$\bar{x}_{t}^{i}=\frac{x_{t}^{i}}{Q W M\left(\mathbf{x}_{t}^{i}\right)}$

下图使用箱线图（boxplot）分别展示了QWM归一化前后的数据情况，其中numbytes的计量单位是MB，其余的都是纯数字：

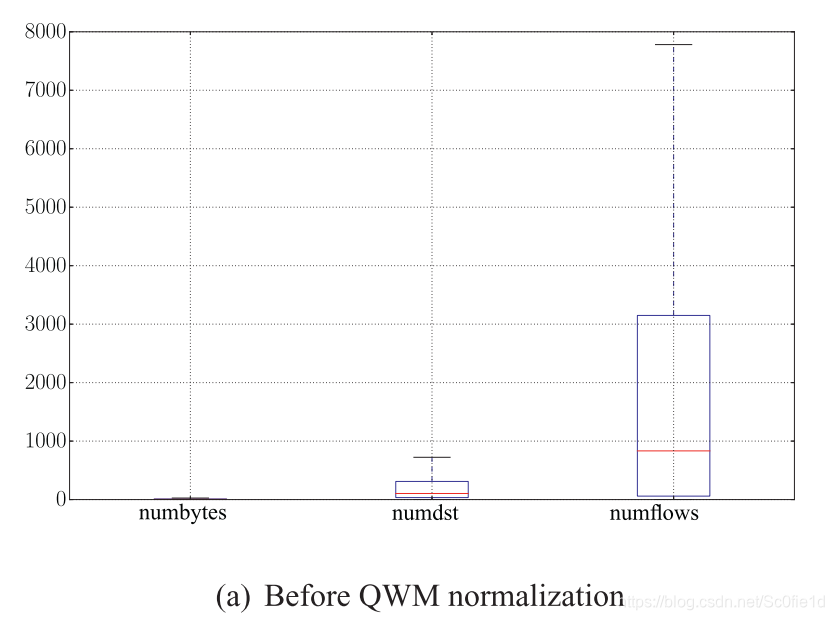
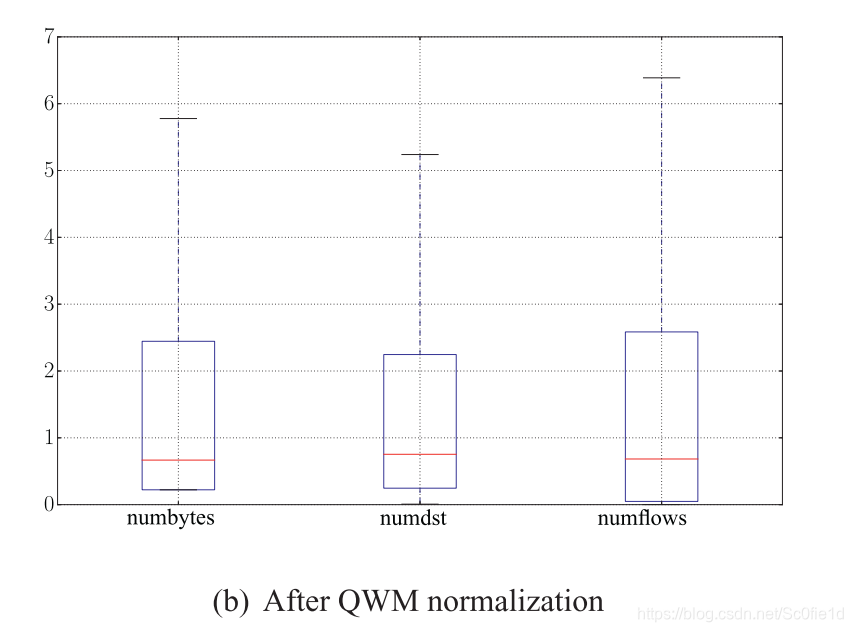
8 计算可疑分数（s1、s2、s3）

每台内部主机 h 在时间 t 时刻的归一化特征向量为（ $\mathbf{x}_{t}$就可以表示在3D特征空间中的一个点）：

$\mathbf{x}_{t}=\left(x_{t}^{1}, x_{t}^{2}, x_{t}^{3}\right)$

其中$\chi_{t}^{i}$表示numbytes（$\chi_{t}^{1}$），numdst（$\chi_{t}^{2}$），numflows（$\chi_{t}^{3}$）。

在每个时刻 t 我们为每台主机计算下面的三个可疑分数：

• $s_{t}^{1}$：距特征空间质心的距离
• $s_{t}^{2}$：特征空间中的移动幅度
• $s_{t}^{3}$：特征空间中运动方向的可能性

（注意三个特征向量和三个分数之间并不是一一对应）下面分别进行讨论。

8.1 距特征空间质心的距离（固定时刻t）

首先计算分数$s_{t}^{1}$，通过该分数可以确定一台主机在时刻t，是否位于多位特征空间的异常区域内。

令${X}_{t}$为时间 t 时，所有内部主机在特征空间中位置的集合（注意这里用大X表示）：

$\mathbf{X}_{t}=\left\{\mathbf{x}_{t}(h): h \in H_{I}\right\}$

下面定义 t 时刻特征空间的质心$\mathbf{c}\left(\mathbf{X}_{t}\right)$：

$\mathbf{c}\left(\mathbf{X}_{t}\right)=\left(\frac{\sum_{h} x_{t}^{1}(h)}{\left|\mathbf{X}_{t}\right|}, \frac{\sum_{h} x_{t}^{2}(h)}{\left|\mathbf{X}_{t}\right|}, \frac{\sum_{h} x_{t}^{3}(h)}{\left|\mathbf{X}_{t}\right|}\right), h \in H_{I}$

其中$x_{t}^{i}(h)$表示主机h特征向量$\mathbf{x}_{t}$的第 i 个特征；$\left|\mathbf{X}_{t}\right|$表示$\mathbf{X}_{t}$的$Cardinality$（集合中元素的个数）。

因此，质心centroid也是一个特征向量，他表示所有主机特征向量的分量的平均值。

最后，我们为每个内部主机h计算特征向量$\mathbf{x}_{t}$与特征空间质心$\mathbf{c}\left(\mathbf{X}_{t}\right)$之间的欧式距离，从而得出$s_{t}^{1}$分数：

$s_{t}^{1}=d_{t}\left(\mathbf{x}_{t}(h), \mathbf{c}\left(\mathbf{X}_{t}\right)\right)=\sqrt{\sum_{i=1}^{3}\left(x_{t}^{i}(h)-c^{i}\left(\mathbf{X}_{t}\right)\right)^{2}}$

8.2 特征空间中的移动幅度（引入时间维度）

下面我们需要确定一种距离度量（其实s1分数也是一种距离度量），该距离度量用于测量内部主机在特征空间中移动的可疑性。

$\mathbf{x}_{t}$从 t-1 时刻到 t 时刻的移动，可以在欧氏空间中用距离向量来表示：

$\mathbf{x}_{t}-\mathbf{x}_{t-1}=\left(x_{t}^{1}-x_{t-1}^{1}, x_{t}^{2}-x_{t-1}^{2}, x_{t}^{3}-x_{t-1}^{3}\right)$

但这种定义方法的缺点是：假设主机A通常的数据上传量是10GB，与标准值仅仅相差１G；而主机B 通常数据上传量是几MB，而某时刻突然变为了100MB，这样主机A的距离向量显然要大于主机B。但是主机A的数据上传量几乎没有增加，而主机B的数据上传量增加了几十倍，显然B更有可能跟数据窃取有关。这种问题是由数量级偏差造成的。

此外仅仅将其与 t-1 时刻相比较也是不合适的。因此设置一个时间窗口是合适的选择，它可以反映主机不断发展的行为基线（evolving behavioral baseline）。

定义$\beta_{t-1}(W)$为特征向量集合$\left\{\mathbf{x}_{t-1}, \ldots, \mathbf{x}_{t-1-w}\right\}$的质心，$W$是时间窗口的大小，$\beta_{t-1}(W)$定义如下：

$\beta_{t-1}(W)=\left(Q_{50}\left(\cup_{j} x_{j}^{1}\right), Q_{50}\left(\cup_{j} x_{j}^{2}\right), Q_{50}\left(\cup_{j} x_{j}^{3}\right)\right)$

其中$j \in\{t-W-1, \ldots, t-1\}$，并且$\beta_{t-1}(W)$中的每个特征，对应特征空间$\mathbf{x}_{t}$的每一个特征$\chi_{t}^{i}$在时间窗口W内的平均值。

下面定义移动向量$\mathbf{m}_{t}$，表示特征点$\mathbf{x}_{t}$和质心$\beta_{t-1}(W)$的相对不同：

$\begin{aligned} \mathbf{m}_{t} &=\frac{\mathbf{x}_{t}-\beta_{t-1}(W)}{\beta_{t-1}(W)} \\ &=\left(\frac{x_{t}^{1}-\beta_{t-1}^{1}(W)}{\beta_{t-1}^{1}(W)}, \frac{x_{t}^{2}-\beta_{t-1}^{2}(W)}{\beta_{t-1}^{2}(W)}, \frac{x_{t}^{3}-\beta_{t-1}^{3}(W)}{\beta_{t-1}^{3}(W)}\right) \end{aligned}$

$\mathbf{m}_{t}$的定义，可以用来表述一个主机从它原先的位置偏离了多少。

最后，用$\mathbf{m}_{t}$的模（magnitude）来表示$s_{t}^{2}$：

$s_{t}^{2}=\left\|\mathbf{m}_{t}\right\|=\sqrt{\sum_{i=1}^{3}\left(\frac{x_{t}^{i}-\beta_{t-1}^{i}(W)}{\beta_{t-1}^{i}(W)}\right)^{2}}$

该分数可以来表示主机相对于其最近的历史情况，其位置改变了多少。

8.3 特征空间中运动方向的可能性

该分数的设计考虑了移动向量的方向，即$\mathbf{m}_{t}$的三个坐标是如何协同变化的，不常规的方向应当被视作可疑行为。

用单位向量 (Unit vector)$\hat{\mathbf{m}}_{t}$来表示$\mathbf{m}_{t}$的方向：

$\hat{\mathbf{m}}_{t}=\frac{\mathbf{m}_{t}}{\left\|\mathbf{m}_{t}\right\|}=\left(u_{t}, v_{t}, w_{t}\right)$

下图展示了1000台主机的$\hat{\mathbf{m}}_{t}$单位向量：

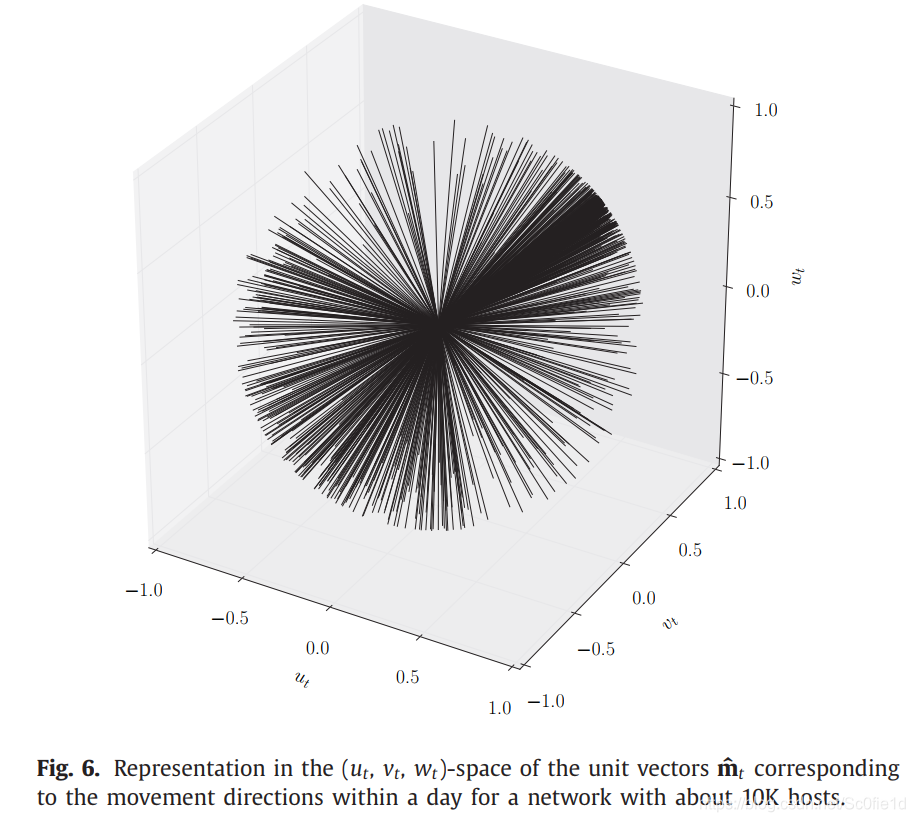
我们注意到，其分布是不均匀的，一些区域的分布密度要远高于其它区域，这意味着朝着某些方向的运动要比其它方向更为常见。

为了更方便地理解其分布，我们使用球面坐标（spherical coordinates）：

$\rho=\sqrt{u_{t}^{2}+v_{t}^{2}+w_{t}^{2}}$
$\varphi=\arccos \left(\frac{w_{t}}{\sqrt{u_{t}^{2}+v_{t}^{2}+w_{t}^{2}}}\right)$
$\theta=\arctan \left(\frac{v_{t}}{u_{t}}\right)$

其中，$\rho\geq0$表示向量的长度（magnitude），$0^{\circ} \leq \varphi \leq 180^{\circ}$，$-180^{\circ} \leq \theta \leq 180^{\circ}$。因此所有的单位向量都有$\rho=1$，只剩下了两个变量。

下图展示了在特定的$(\varphi,\theta)$下，内部主机数量的直方图：

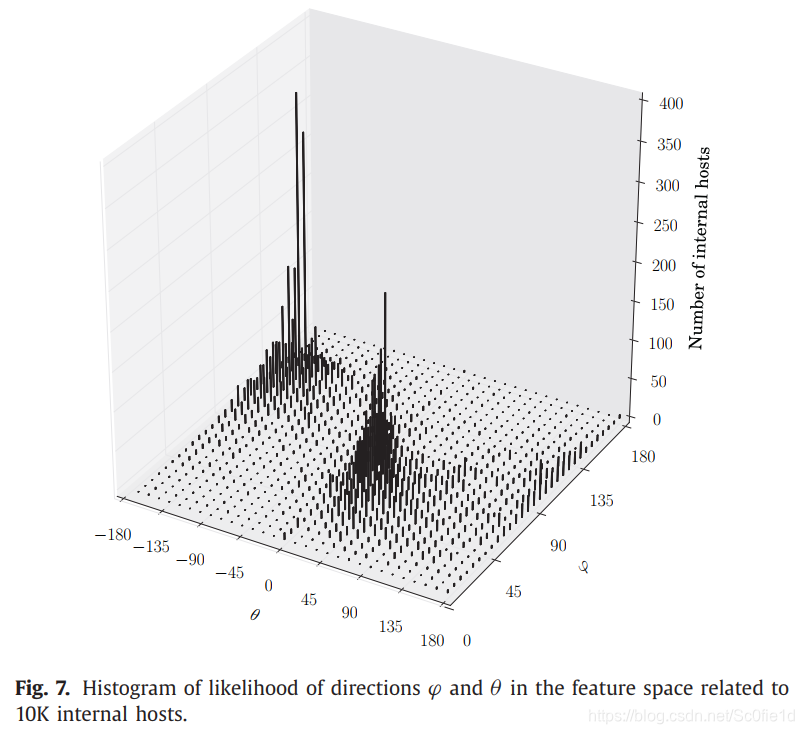
显然，大多数内部主机仅沿可能方向的一小部分移动。 因此，朝着不太常见方向的运动代表着可疑行为。特别是，我们可以观察到两个具有相当高密度的空间区域。

为了更好地理解上述直方图，我们将其表示为2D投影图：

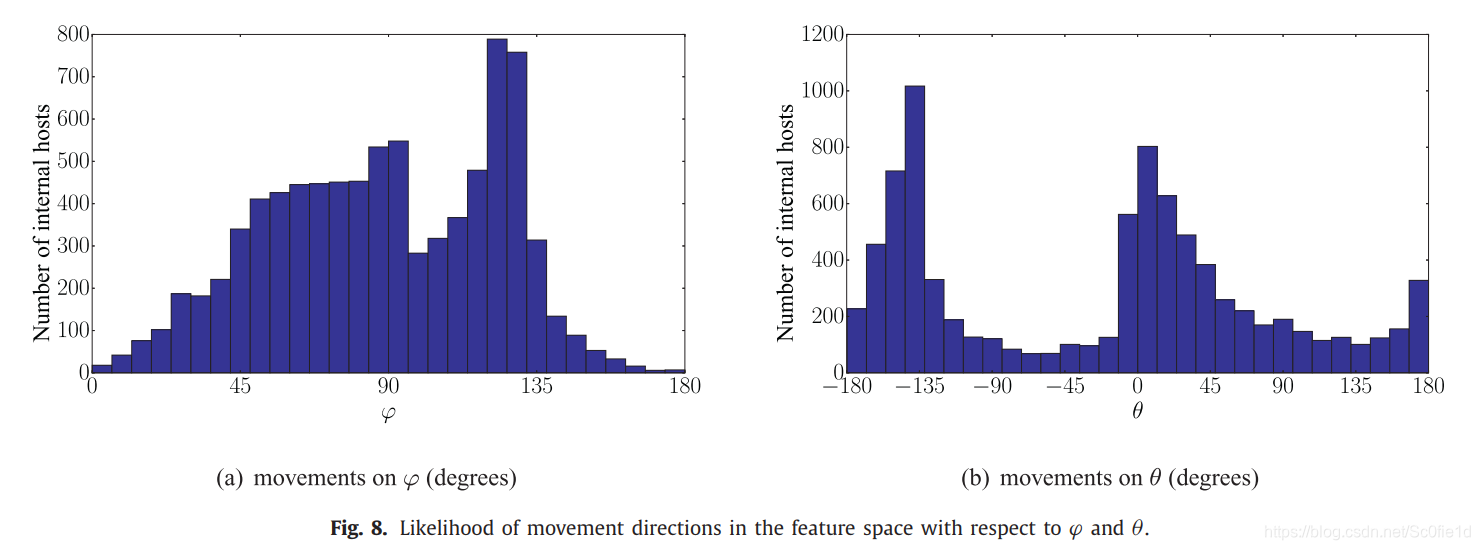
接下来定义分数$s_{t}^{3}$：

$s_{t}^{3}=1-\operatorname{Pr}\left(\hat{\mathbf{m}}_{t}\right)$

其中$\operatorname{Pr}\left(\hat{\mathbf{m}}_{t}\right)$表示特征空间中特定方向的可能。$1-\operatorname{Pr}\left(\hat{\mathbf{m}}_{t}\right)$为其对立事件，称之为在特征空间中向某个方向移动的不可能性（unlikelihood）。因此该分数越高，主机的移动方向就越可疑。

8.4 计算最终分数

最终分数$S_{t}$是三个分数的线性组合：

$S_{t}=\sum_{j=1}^{3}\left(\delta_{t}^{j} \cdot s_{t}^{j}\right)$

其中$\delta_{t}^{j} $是和对应分数相关的归一化权重。因为三个分数有不一样的界限、规模和分布，因此我们使用QWM定义$\delta_{t}^{j} $来将它们归一化：

$\delta_{t}^{j}=\frac{\sum_{k, k \neq j} Q W M\left(s_{t}^{k}\right)}{\sum_{k} Q W M\left(s_{t}^{k}\right)}, k \in\{1,2,3\}$

我们框架的最终输出是一个内部主机列表，该列表关于最终分数$S_{t}$按降序排列。

9 实验评估

评估环境为一个具有10K台主机的网络，将本文的框架在其中运行了五个月。

评估的目的主要是下面三个方面：

• 时间和存储空间方面的性能消耗
• 检测能力
• 对于不同类型主机、不同大小文件泄露的敏感度

9.1 实验测试平台和框架性能

回顾之前在chapter 6中谈到的检测框架的五个步骤：流量收集和存储、特征提取、特征归一化、可疑分数计算和排名。每个步骤分别如下实现：

• 流量收集和存储由nprobe实现，它可以用来在大型网络环境中收集流量记录（flow records）。
• 特征提取、特征归一化用Go语言实现
• 可疑分数计算、排名用Python实现

每隔时间T=1天进行一次采样，也就是说每天生成一次排名。时间窗口大小W=14天。

所收集到的流量记录如下所示：

性能和内存需求：

9.2 检测手工注入的数据窃取

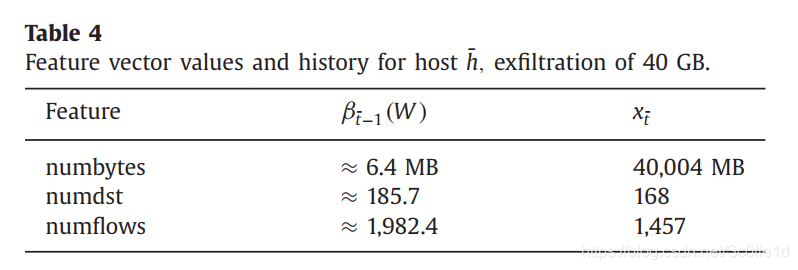
首先随机选择某一天，并且主机在这一天的数据上传量和平均水平相当。然后我们执行两个实验来模拟数据窃取，数据窃取量分别为40GB和9GB。

• 知识点：bin in statistics；直方图中的类别

经过计算，关于分数$s_{t}^{3}$中的直方图，我们选择的直方图块数的最优大小是：$\theta$十个bin，$\varphi$五个bin。

下面是对于两个数据窃取的检测结果：

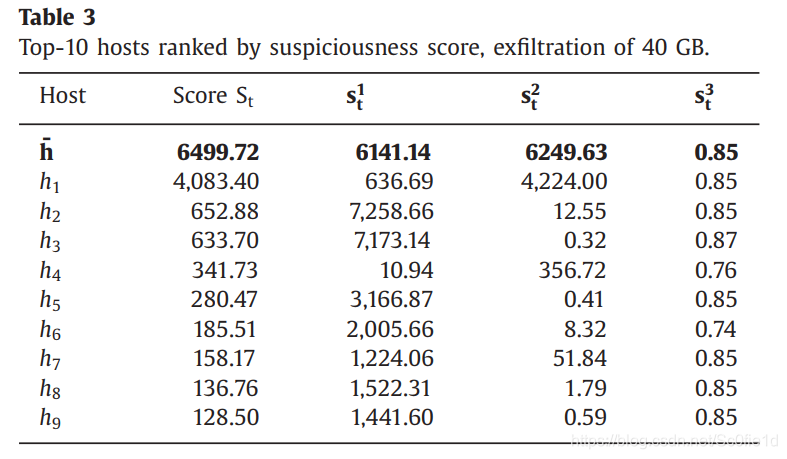
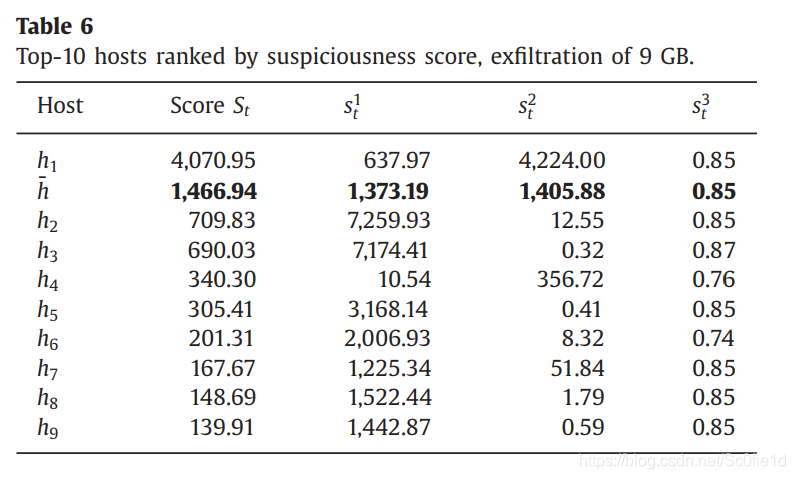
9.3 敏感度分析和对比评估

若数据泄露主机140天以来的平均排名大于50，那么对于只能分析50台主机的系统来说，就难以检测到威胁。

接下来我们在不同类别的主机上，验证所提方法的有效性。

我们利用前面提到的“每台内部主机上传的字节数（per-day）”，其分布为重尾分布。实验室长为140天，每一天，我们从中选出七个具有不同上传量的主机，分别对应一个特定的分位数：0.01, 0.05, 0.25, 0.50, 0.75, 0.95, 0.99 （即将所有的主机按照数据上传量由少到多排列，r0.01表示第百分之一个主机，因此这些主机的正常数据上传量是依次递增的）。这使得我们可以评估不同的低、中、高上传者。然后，我们向这7台主机中分别注入信息窃取攻击，每天每台主机的信息窃取量包括以下八种：50 MB, 100 MB, 200 MB, 500 MB, 1 GB, 2 GB, 5 GB and 10 GB。

该实验允许我们对所有可能的信息窃取，进行全频段的分析，从low-and-slow到burst数据泄露。

普通的方法：仅仅按照数据上传量来给主机进行排名。接下来，我们分别使用我们的排名方法和普通的排名方法，对7种主机、八种数据大小全部计算了分数。对比图如下：

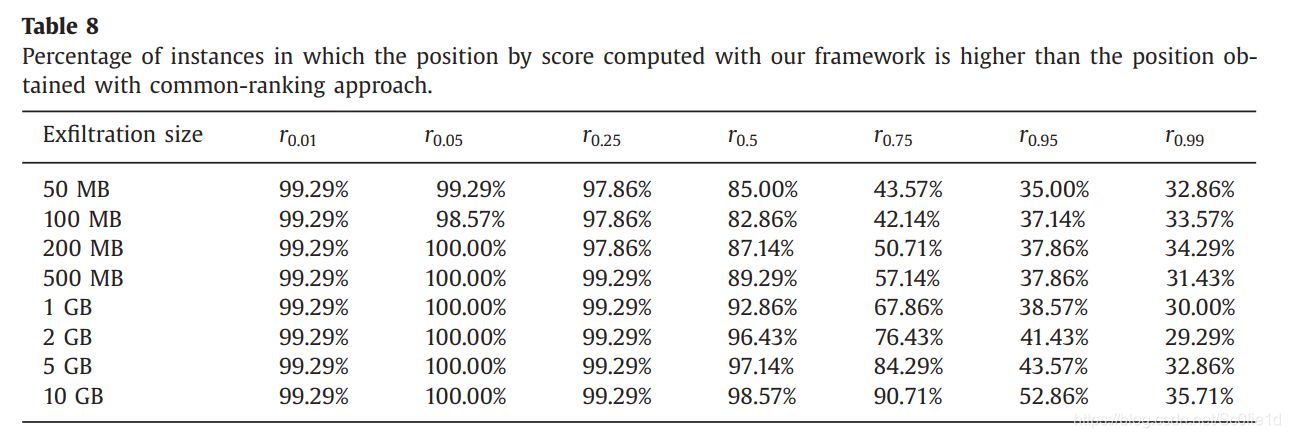
每一列代表不同的主机，每一行代表不同的数据大小。每个单元格表示我们的方法优于普通方法的比率。比如99.29%表示在140天中，有139天本文提出的方法要优于普通方法。（i.e.会把可疑主机放在更高的排名位置）

图中我们可以看出r0.75和r0.95因数据大小不同，结果也不同。但是r0.99偏爱常规的检测方法，这是因为r0.99平时上传的数据量比较大，因此常规方法比较容易将其放在排名较高的位置（而不管数据泄露的多少）；但是本文的方法将数据泄露量作为日常数据上传的增量时，就显得微不足道了，所以较难检测出数据泄露的存在。

因此可以得到本文方法的优点：

• 相较于普通方法，本文的方法在大多数情况下表现较好
• 它将原本不会被考虑的主机标注为了可疑，因为普通的方法经常会让大数据上传者占据主导地位。（废话？小数据上传者的检测还不容易吗？）

下面，分别为两种方法计算排名的中位数：

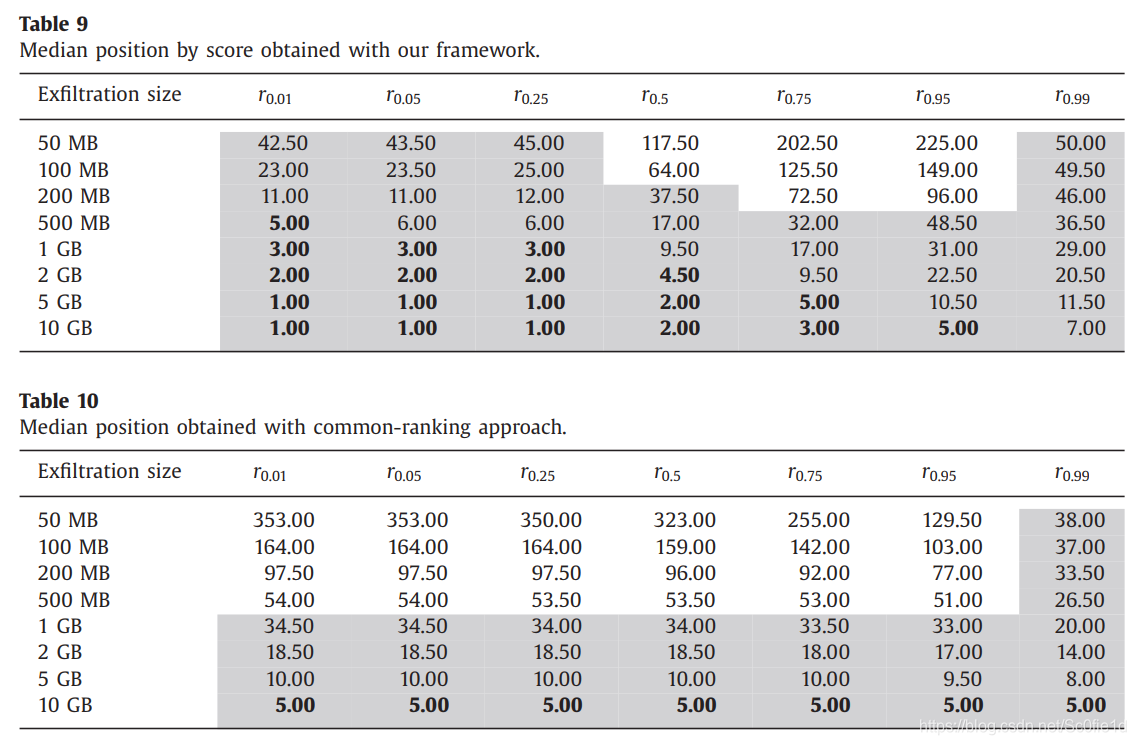
每个单元的数据：rx.xx表示140天中每一天对应的主机，该主机每天根据计算分数会有一个排名，每个单元的数表示这些排名的中位数。如42.50就表示在140天中，至少有一半的时间，其排名是高于42.5的。

根据不同的环境，分析威胁的能力也不同。假设第一种环境每天能分析50台主机，我们在途中用灰色表示出来；第二种环境每天能处理5台主机，我们在图中用加粗字体表示出来。比如53.50未被标位灰色，因为一共能处理50台主机，而有一半以上的情况该主机的排名是在50名开外的，在这些情况下、在第一种环境中查表查不到这台主机，因此我们认为这种情况是我们的方法没有有效处理的情况。

9.4 结果总结

相对于普通方法（common-ranking）的提升在于：

• 对于大部分主机，都可以快速（10K host、140millions flows，in 2 mins）识别low-and-slow数据窃取
• 对于中、小量的数据上传者来说，检测效果明显优于普通方法
• 不会像普通方法那样，让大数据量上传者始终占据排名前列
• 即便是中、小量的数据上传者，也可以被识别为最可疑的对象

对比Table 9和10的结果，可以看出common-ranking在数据窃取量低于500MB每天时，在大多数情况下都无法检测。

此外，根据Table 9，如果攻击者想绕过我们的检测系统，那么需要落在未被标位灰色的单元格内。这要求攻击者一方面要了解内部网络是数据传送情况，将数据窃取点选在r0.5-r0.95的主机之间，这不仅取决于单台主机，同时也取决于网络中其他主机的数据传送量；另一方面要控制每天的数据窃取大小。因此想要绕过我们的系统是非常困难的。

10 思考

10.1 存在的问题

• 仅仅三个特征未免过于简单
• 实验环境中的主机在评估期间一定会遭受APT攻击吗？人为加入攻击
• 没有时间复杂度分析
• 对于大量数据上传者主机上的数据泄露检测效果不佳

10.2 未来的研究方向

对于使用其它安全资产的关联系统，比如来组IDS的data flows和alerts，可以集成到我们的系统中。